Right triangles and trigonometry unit test – Embark on an illuminating journey through the captivating world of right triangles and trigonometry, as we delve into the intricacies of this fundamental unit test. Prepare to unravel the secrets of trigonometric ratios, identities, and their myriad applications, equipping yourself with the knowledge and skills to conquer any challenge that lies ahead.
Our exploration begins with a thorough examination of right triangle properties, where the Pythagorean theorem reigns supreme. We will uncover the intricate relationships between sides and angles, empowering you to solve complex problems with precision. The trigonometric functions—sine, cosine, and tangent—will become your allies as we explore their definitions, relationships, and applications.
Right Triangle Properties
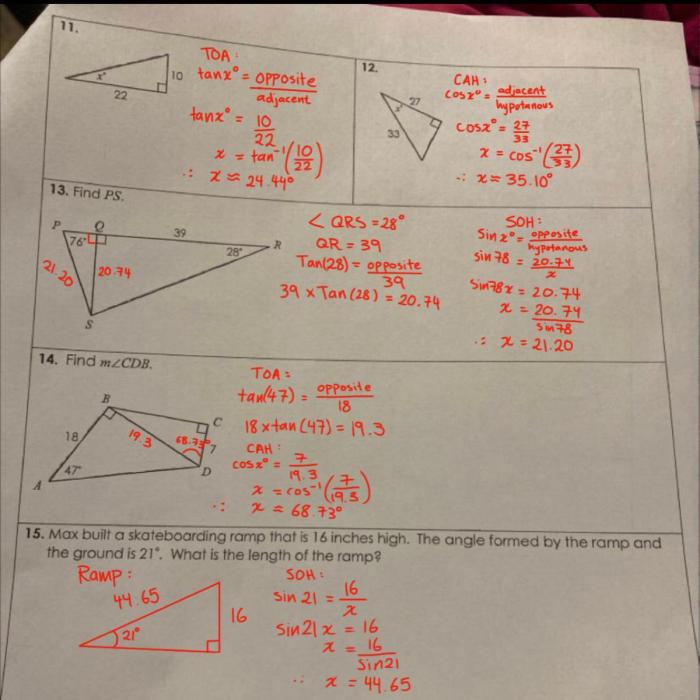
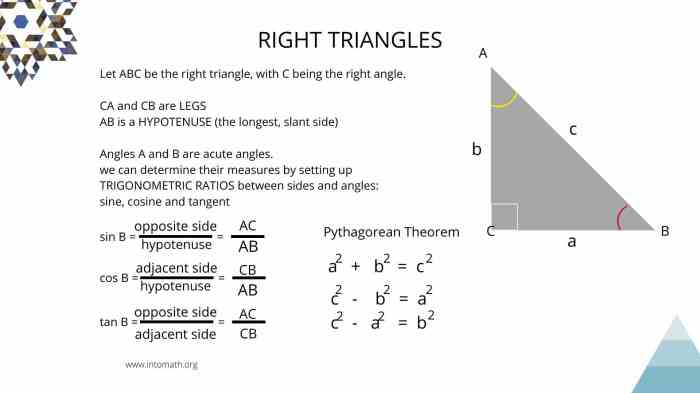
Right triangles are characterized by having one right angle (90 degrees). They possess unique properties that make them important in various applications. One of the most fundamental properties is the Pythagorean theorem, which states that the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides.
In addition to the Pythagorean theorem, right triangles also exhibit relationships between their sides and angles. These relationships are expressed through trigonometric ratios: sine, cosine, and tangent. The sine of an angle is the ratio of the length of the opposite side to the length of the hypotenuse, the cosine is the ratio of the length of the adjacent side to the length of the hypotenuse, and the tangent is the ratio of the length of the opposite side to the length of the adjacent side.
Understanding these properties and relationships is essential for solving problems involving right triangles, such as finding missing side lengths, angles, or areas.
Trigonometric Functions: Right Triangles And Trigonometry Unit Test
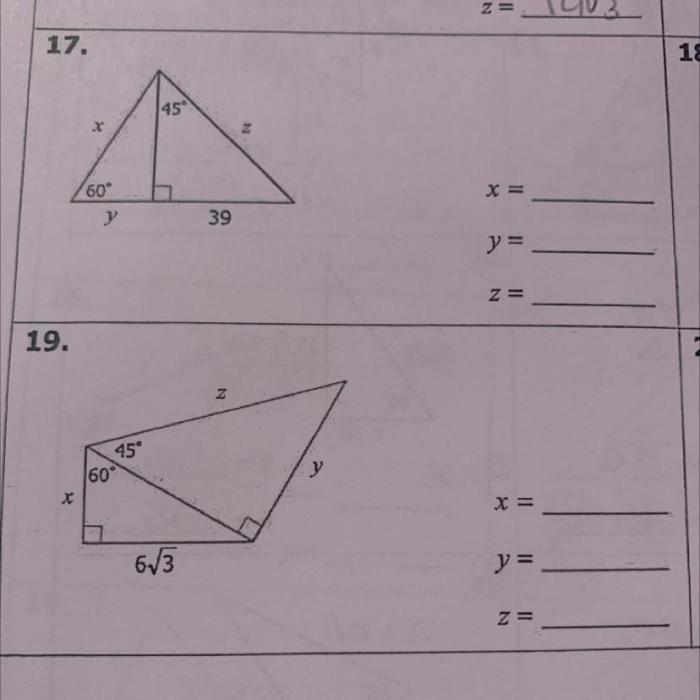
Trigonometric functions are mathematical functions that relate the angles of a right triangle to the ratios of its sides. The six trigonometric functions are sine, cosine, tangent, cosecant, secant, and cotangent.
These functions can be calculated using the unit circle, which is a circle with radius 1 centered at the origin of the coordinate plane. By placing a right triangle inside the unit circle, we can define the trigonometric functions as follows:
- Sine (sin) = y-coordinate of the point on the unit circle
- Cosine (cos) = x-coordinate of the point on the unit circle
- Tangent (tan) = y-coordinate / x-coordinate of the point on the unit circle
- Cosecant (csc) = 1 / sine
- Secant (sec) = 1 / cosine
- Cotangent (cot) = 1 / tangent
The values of the trigonometric functions can be found for any angle using a calculator or trigonometric tables.
Trigonometric Identities
Trigonometric identities are equations that involve trigonometric functions and are true for all angles. These identities can be used to simplify trigonometric expressions and solve equations.
Some of the most common trigonometric identities include:
- Pythagorean identity: sin²θ + cos²θ = 1
- Angle addition identity: sin(A + B) = sinA cosB + cosA sinB
- Angle subtraction identity: sin(A – B) = sinA cosB – cosA sinB
- Double-angle identity: sin(2θ) = 2 sinθ cosθ
- Half-angle identity: sin(θ/2) = ±√((1 – cosθ) / 2)
These identities are essential for solving a wide range of trigonometric problems.
Applications of Trigonometry
Trigonometry has numerous applications in various fields, including:
- Surveying and navigation:Determining distances and angles in order to create maps and charts.
- Architecture and engineering:Designing and constructing buildings, bridges, and other structures.
- Physics and astronomy:Studying the motion of objects and the behavior of light and other electromagnetic radiation.
Trigonometry is an essential tool for solving problems in these and many other fields.
Unit Test Preparation
To prepare for the unit test on right triangles and trigonometry, it is important to review the following concepts and skills:
- Pythagorean theorem
- Trigonometric ratios (sine, cosine, tangent)
- Trigonometric functions (sine, cosine, tangent, cosecant, secant, cotangent)
- Trigonometric identities
- Applications of trigonometry
Students should also practice solving problems involving right triangles and trigonometry. Sample problems and practice exercises can be found in the textbook and online resources.
FAQ Resource
What is the Pythagorean theorem?
The Pythagorean theorem states that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides.
What are the trigonometric functions?
The trigonometric functions are sine, cosine, tangent, cosecant, secant, and cotangent. They are used to relate the angles of a right triangle to the lengths of its sides.
What are trigonometric identities?
Trigonometric identities are equations that are true for all angles. They can be used to simplify trigonometric expressions and solve equations.
